Die perfekte Wurfmaschine

Mein Physik Studium hat mich einiges gelehrt - vor allem wie man tolle, große Beschleuniger baut. So verrückt es auch klingen mag, im dritten Semester lernt man dazu das mathematische Werkzeug wie man die perfekte mittelalterliche Wurfmaschine baut.

Ein Trebuchet, von lat. trabatium, auch Blide oder Tribock genannt, ist eine altertümliche Belagerungsmaschine, die im vierten bis dritten Jahrhundert vor Christus erstmals in China als Zugblide auftrat. Bei einer Zugblide wird das Geschoss nicht mit einem am Hebel angebrachten Gegengewicht beschleunigt, sondern die nötige Kraft, um das Geschoss auf hohe Geschwindigkeiten zu bekommen, wird von Personen geliefert, die den kurzen Hebelarm an Seilen nach unten ziehen. Im sechsten Jahrhundert brachten Kreuzfahrer und Händler die Zugblide in den Mittelmeerraum.

Erst ab dem 12. Jahrhundert kamen verbesserte Maschinen mit pendelndem Gegengewicht in Westeuropa als Belagerungswaffen zum Einsatz und konnten sich sogar später einige Zeit lang gegen Schießpulver behaupten. Das Trebuchet mit Gegengewicht hatte den großen Vorteil, dass schwerere Geschosse mit gleichbleibender Kraft beschleunigt werden konnten, weshalb das Ergebnis präziser und nicht mehr von der variierenden Zugleistung der Personen abhing.

Originale Pläne oder Maßangaben von mittelalterlichen Wurfmaschinen sind leider verschollen, weshalb man heute die Maße von Trebuchets meist aus Gemälden rekonstruieren oder sich mit plausiblen Annahmen abfinden muss.

Um eine solche plausible Annahme soll es hier gehen. Es soll versucht werden mit einem einfachen physikalischen Modell Differentialgleichungen abzuleiten, die über ein Optimierungsverfahren auf die optimalen Maße eines Trebuchets führen. Vorweg: Das Modell funktioniert erstaunlich gut und liefert Verhältnisse von Maßen, die mit denen aus alten Abbildungen gut übereinstimmen. Das Modell soll später dazu dienen, ein optimales Trebuchet nach einer Bauweise aus dem 12. Jahrhundert zu rekonstruieren. Die reale Wurfweite des Nachbaus soll das Modell auf Richtigkeit überprüfen und klären, ob es sich tatsächlich um eine geeignete Konstruktion aus dem frühen Mittelalter handelt.

Alle Rechnungen wurden mit Mathematica durchgeführt. Wer sich selbst auf die Suche nach dem optimalen Trebuchet begeben möchte oder meine Maße dazu benutzen möchte, eine eigene Wurfmaschine nachzubauen, kann den Quellcode und die Maßangaben hier herunterladen. Doch bevor ich auf meine Konstruktion näher eingehe, möchte ich die Funktionsweise eines Trebuchets erklären.

Folgende Maße sind für die Simulation eines Trebuchets wichtig:

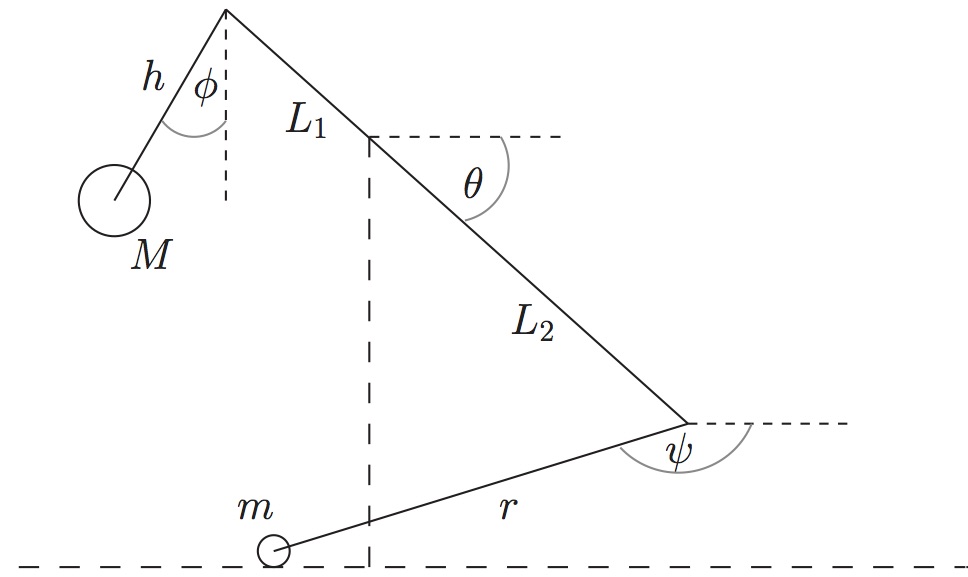
Der Winkel Phi wird zwischen Vertikale und der Aufhängung h des Gegengewichts M gemessen. L1 und L2 sind die jeweiligen Abmessungen des Wurfarms bis zum Drehpunkt. Zwischen der Horizontalen und dem Wurfarm befindet sich der Winkel Theta. Der Winkel Psi misst die Auslenkung zwischen der Horizontalen und der Wurfschlinge mit der Länge r. Das Geschoss hat die Masse m. Außerdem wird das Trägheitsmoment des Wurfarms mit I parametrisiert. Als erste Näherung kann hier das Trägheitsmoment einer langen Stange (1/12 µ (L1+L2)^2) verwendet werden, wobei µ die Masse des Wurfarms ist. In der Simulation wird ein Trägheitsmoment eines optimierten Wurfarms verwendet, d.h. der Wurfarm ist unten dick und läuft zum Ende hin spitz zu. So wird gewährleistet, dass die längere Strecke L2 weniger zum Trägheitsmoment beiträgt.

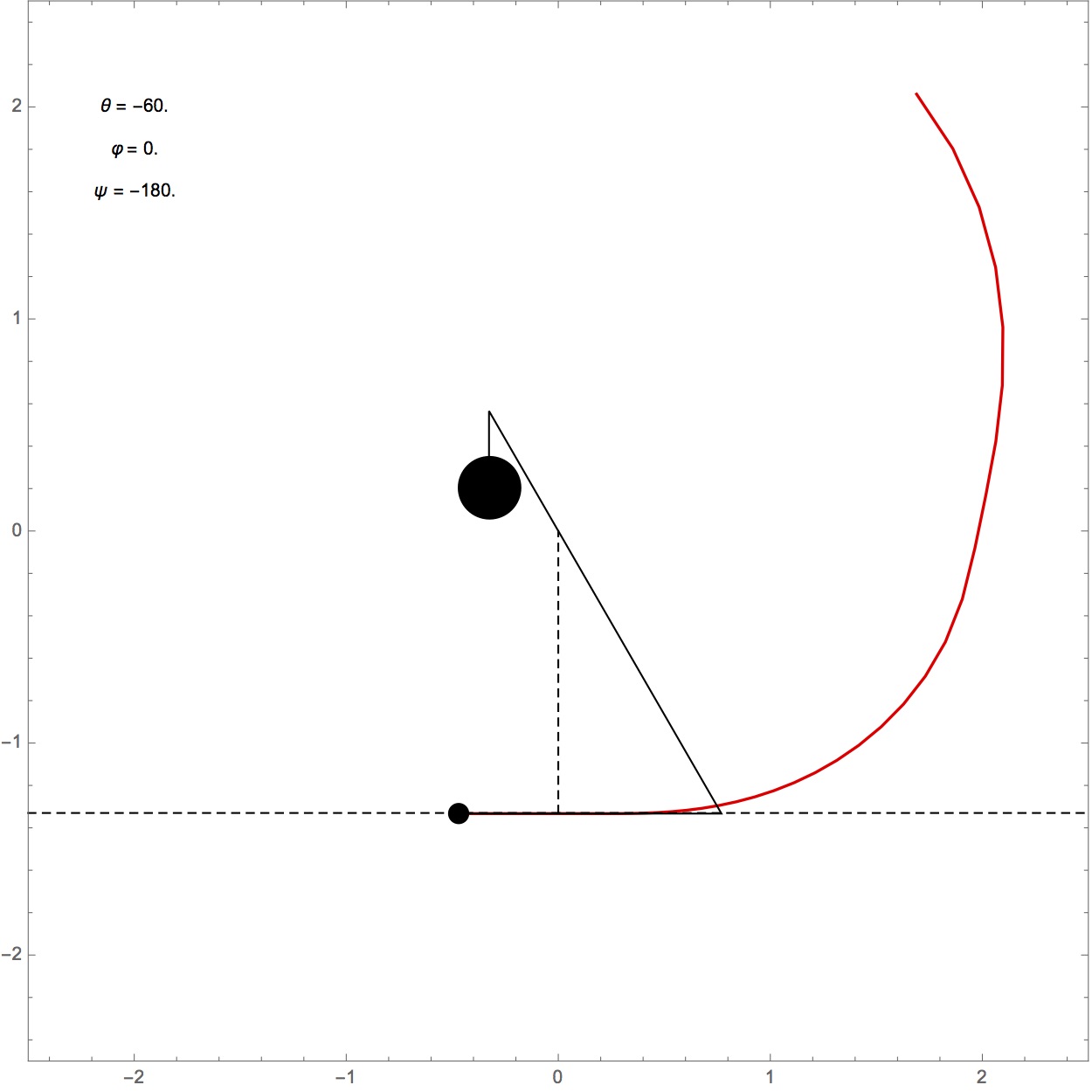
Im ersten Schritt befindet sich das Geschoss auf dem Boden und das Gegengewicht am höchsten Punkt. Die Geschwindigkeit des Geschosses und des Gegengewichts ist null, die ganze Energie der Anordnung ist in der potentiellen Energie des Gegengewichts gespeichert.

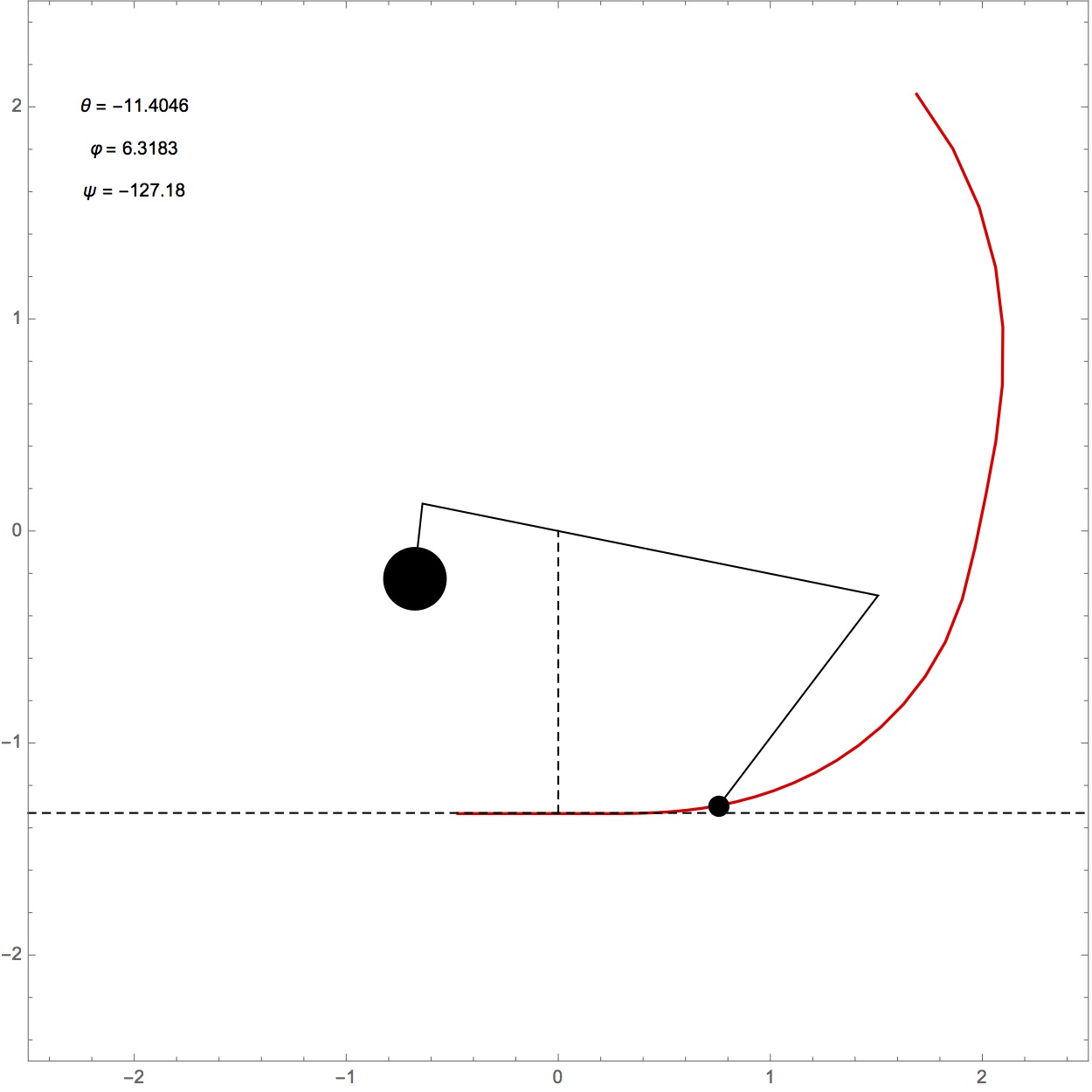
Nachdem das Gegengewicht losgelassen wird, fällt es aufgrund der Erdanziehung senkrecht nach unten. Der Wurfarm folgt der Bewegung des Gegengewichts und beschleunigt das Geschoss. Anfangs wird das Geschoss von der Schlinge auf dem Boden gezogen, bis es nach einer gewissen Zeit den Boden verlässt und sich auch in die vertikale Richtung bewegen kann. Es stellt sich heraus, dass das Ziehen des Geschosses auf dem Boden einen erheblichen Beitrag zur Wurfweite liefert. Der Boden verringert den Radius der Trajektorie am Anfang, weshalb das Geschoss einen kleineren Beitrag zum Trägheitsmoment erzeugt.

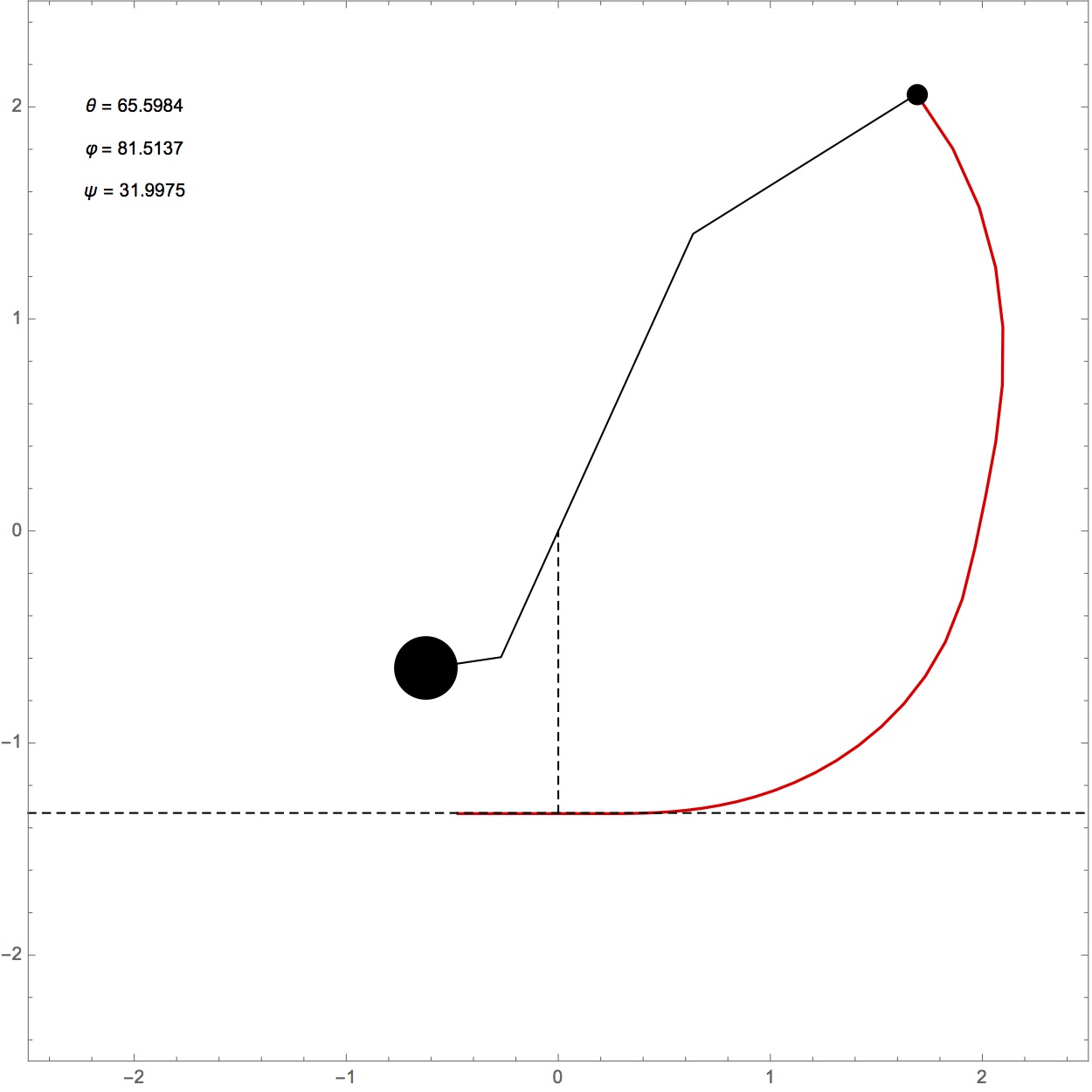
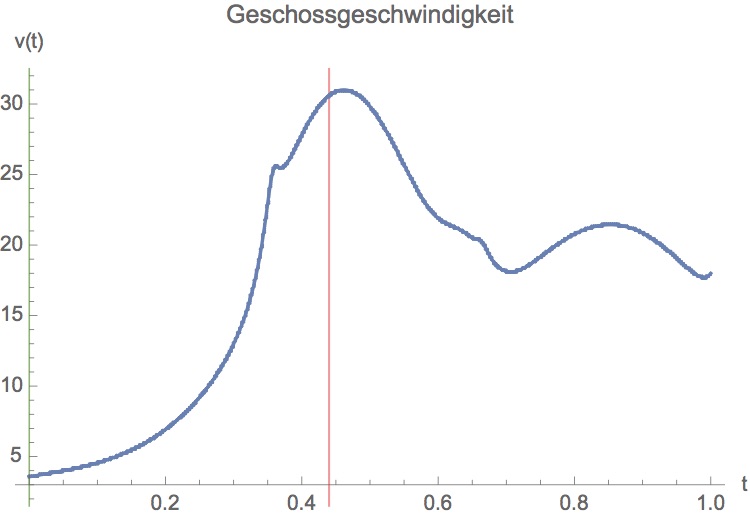
Abwurfphase: Das Gegengewicht hat nahezu seinen tiefsten Punkt und das Geschoss hat die höchste Geschwindigkeit erreicht. In dieser Phase tritt ein interessantes Phänomen auf, das sogenannte "Pumpen": Beim Pumpen erhöht sich die Geschossgeschwindigkeit durch die besondere Geometrie des Trebuchets schlagartig (siehe Diagramm zur Geschossgeschwindigkeit v(t)). Das ist auch der Grund warum ein Trebuchet als Wurfmaschine so effektiv ist. Die nachfolgende Animation verdeutlicht den Pumpeffekt.

Die folgende Animation wurde mit Mathematica für die plausiblen Abmessungen eines realen Trebuchets erstellt. Alle Unterlagen lassen sich hier herunterladen.

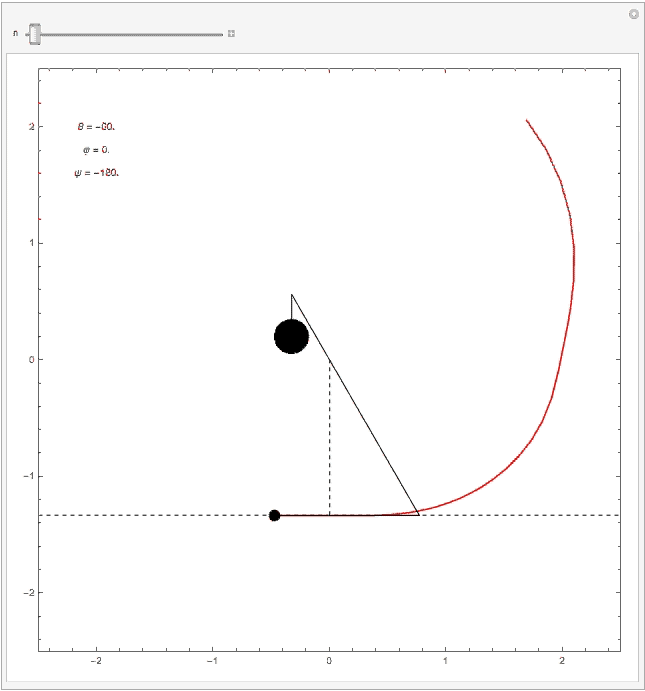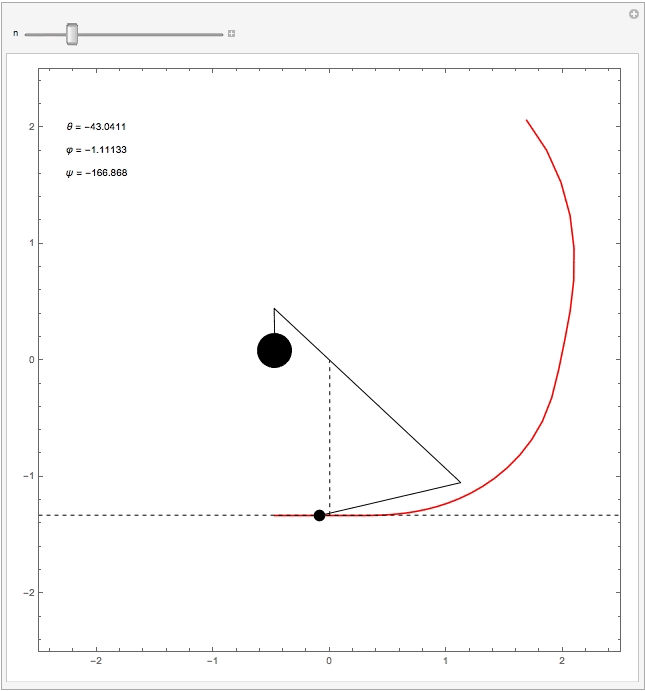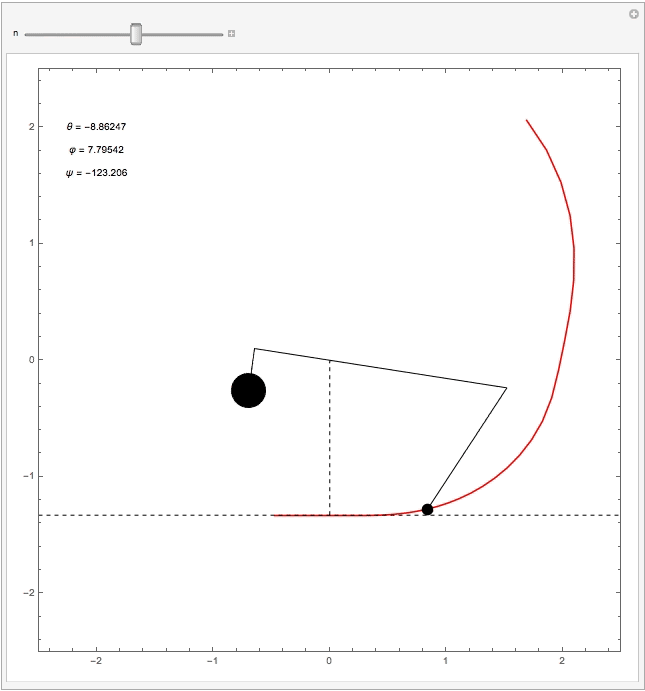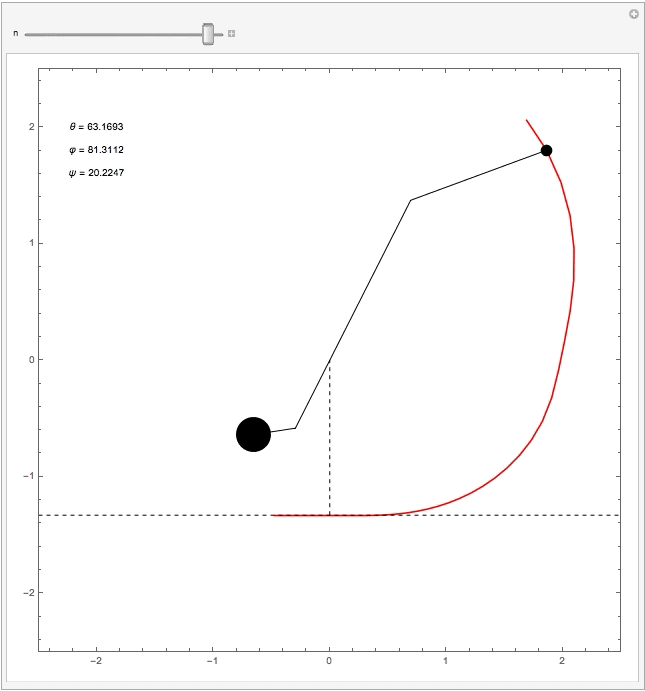
Geschossgeschwindigkeit in Abhängigkeit der Zeit. Man sieht deutlich, dass sich die Geschwindigkeit vor dem Abwurf schlagartig erhöht (rote Linie). Die erste Spitze vor dem globalen Maximum ist dem Pumpeffekt des Trebuchets geschuldet.

Mit dem verlinkten Mathematica Skript können durch ein Optimierungsverfahren alle relevanten Parameter, d.h. die optimale Länge der Aufhängung des Gegengewichts, die Wurfarm- und Schlingenlänge in Abhängigkeit der Massen berechnet werden. Dazu wird eine Lagrangefunktion aufgestellt, die den Zusammenhang aller physikalisch relevanten Größen beschreibt. Über die Euler-Lagrange-Gleichung werden die gekoppelten Differentialgleichungen von Theta, Psi und Phi berechnet, die anschließend mit Randbedingungen numerisch gelöst werden. Durch Variation der verschiedenen Parametern kann die Wurfweite berechnet werden. Die Wurfweite wird dann in Abhängigkeit aller Parameter maximiert.

Zusammenfassend hier die weniger interessanten Diagramme zur maximalen Wurfweite und zu den komplizierten Winkelfunktionen. Die maximale Wurfweite mit einem Gegengewicht von 50kg und einem Geschossgewicht von 0.5kg beträgt etwa 100m.

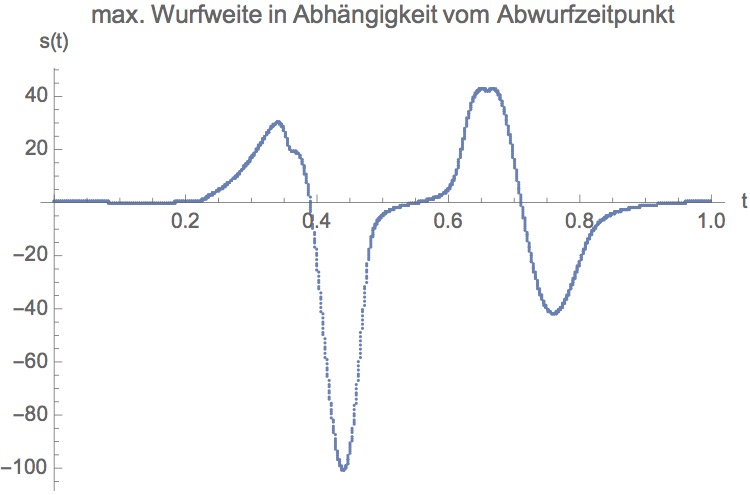
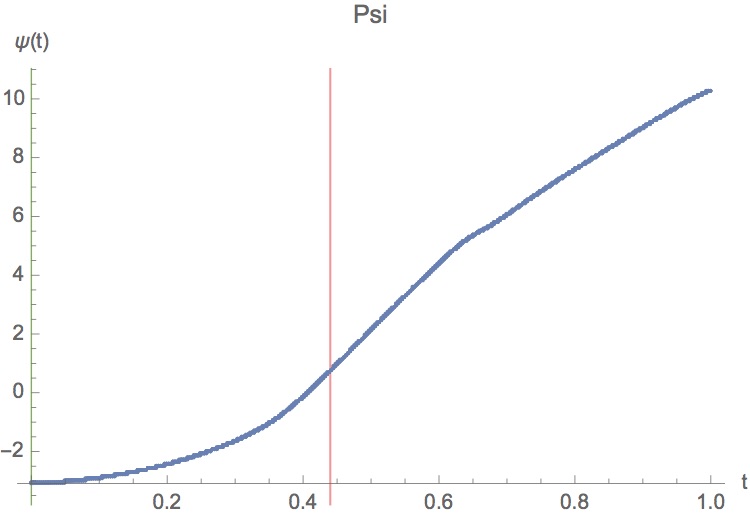
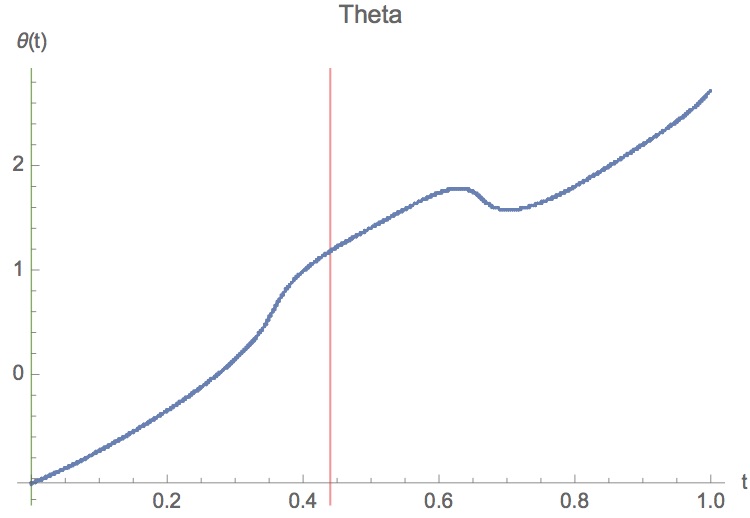
Mit den optimierten Parametern konnten daraufhin Zeichnungen in AutoCAD erstellt werden. Diese Zeichnungen sollen später dazu dienen das Trebuchet aus Holz nachzubauen und die Wurfweite mit den Rechnungen zu vergleichen.